La estadística es una descripción numérica qué además sirve para tomar decisiones a partir de muestras poblacionales y analizar la variedad de fenómenos aleatorios .
¿Cómo se hace?
Para ésto, debe existir una situación para analizar la realidad.
 |
| FIG.1 Toda REALIDAD cantitativa y cualitativa se deriva de un modelo. |
- Determinar el modelo que describa los datos
- Determinar el modelo que explica los datos
- Generalizar conclusiones a la situación real
!=
- Un modelo es una abstracción simplificada de una realidad más compleja, lo cuál no quiere decir que sea una REALIDAD TOTAL.
- No se puede hacer estadística sin la ayuda de la lógica.
- Si los datos se explican en contextos diferentes, ésos datos obedecen al contexto real que se manejar.
- La estadídtica busca la metodología para evaluar discrepancias; una discrepancia es un valor inferior por explicar.
- Todo profesional debe analizar datos.
 |
| FIG.1 La realidad desde la investigación cantitativa. |
No sirve el modelo cuando...
-Existen distintas explicaciones
-La discrepancia no se pueda explicar
-El promedio es 0
-Relativamente tiene poca variabilidad
-Variabilidad sea constante
-Que ni el modelo ni la discrepancia estén corelacionados.
-Que el dato del residuo sea racionable (Ley de Hauss).
!=
-Tener en cuenta el contexto para plantear el modelo.
-Formular el modelo.
-Definir claramente los parámetros del modelo.
-Seleccionar los parámetros en procedimiento.
-Utilizar los residuos para analizar las discrepancias.
-Se utilizan en algunos casos histogramas como por ejemplo para analizar en una población el sexo más dominante.
-El promedio no es una recta
!=
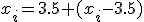
Sus variables son:
P_{t}: Precipitación
P(t): Tendencia con respecto al tiempo
R_{1}: Estacionalidad en el tiempo
Para lo anterior,se hizo autocorelaciones con respecto al patrón estacional .
!=
Grafología (FDA): estadística cartesiana en la escritura
-Que el dato del residuo sea racionable (Ley de Hauss).
!=
-Tener en cuenta el contexto para plantear el modelo.
-Formular el modelo.
-Definir claramente los parámetros del modelo.
-Seleccionar los parámetros en procedimiento.
-Utilizar los residuos para analizar las discrepancias.
-Se utilizan en algunos casos histogramas como por ejemplo para analizar en una población el sexo más dominante.
-El promedio no es una recta
Ejemplos de modelos
-El promedio de un alumno con respecto a un grupo de estudiantes de clase que sacaron en promedio 3.5
-En las universidades, en las facultades con dependencia al semestre exite un número de estudiantes que descertan académicamente; las ecuaciones son las siguinetes:
!=
-Las variables de los semestres son:
1: Primer semestre
0:Segundo semestre
2:Sumatoris de los dos semestres
ε= variable independiente
-Los biólogos utilizan una derivada con base a los logaritmos naturales para averiguar por ejemplo la producción de bagre que hay en una laguna con respecto a la talla y el sexo.
1: Primer semestre
0:Segundo semestre
2:Sumatoris de los dos semestres
ε= variable independiente
-Los biólogos utilizan una derivada con base a los logaritmos naturales para averiguar por ejemplo la producción de bagre que hay en una laguna con respecto a la talla y el sexo.
-En San Andrés Islas, hay precipitaciones a lo largo del año a excepción entre Febrero y Abril. Pero en Novienmbre y Diciembre llueve frecuentemente.
!=
Sus variables son:
P_{t}: Precipitación
P(t): Tendencia con respecto al tiempo
R_{1}: Estacionalidad en el tiempo
Para lo anterior,se hizo autocorelaciones con respecto al patrón estacional .
!=
-El promedio no es una recta.
Grafología (FDA): estadística cartesiana en la escritura
-Cada punto en la palabra se representa en coordenadas en dependencia al tiempo en segundos t(seg)
COORDENADAS:
DERIVADAS:
ACELERACIÓN:
BÚSQUEDA DE LA SEÑAL GRAFOLÓGICA:
BIBLIOGRAFÍA
GARZÓN M. Carlos Arturo (2012). ¿Qué nos dicen los datos? [Apuntes], Santafé de Bogotá D.C., Colombia:Universidad de La Salle (Sede Centro): Dept. Ciencias Báscias y Facultad de Ingeniería.
